
Klon or Klones? A legend under the lens
Few pedals exist out there whose legendary status and hype have peaked as high as that of Klon’s Centaur overdrive. This pedal, worth a couple
We’ve all fallen in love at some point in our life with a well-modulated guitar sound, likely more than once. It’s something that goes beyond the grittiness of distortion or the vastness of reverbs and delays. It’s a harmonised shimmer, a goose-bumps raising feeling of longing and nostalgia which catches your breath and makes you dream.
Who doesn’t love that?
Yet, the art of modulation often remains a mystery for many approaching guitar playing from a musical and creative perspective. The sheer number of available pedals and the different options they offer, is enough to make one’s head spin. And even though we might know, deep down, the exact sound that we are looking for, it is often not just as clear what will get us there.
To help you down that road, here is an in-depth look into everything you need to know about modulation effects: how they work, how to use them, and which is the best for you between flangers, phasers, and choruses. As a good starting point, have a listen and compare the sound of all three types in the player below.
Sound waves, as complex as they might appear at first sight, are much like any other wave you have encountered in your life. Imagine laying on the beach looking at the sea coming in, or dropping a pebble in a pond. In both cases you will observe ripples pushing the water’s mass both above and below the line of the surface. Most waves found in nature (including energy waves such as light) follow the same movement pattern.
Sound waves are also not so different in concept, and share most of the characteristics used to describe them with the waves that we see in water. However, one important difference is the way they move: instead of pushing mass or energy above and under along their path, they push it back and forth. A source creating a sound will still behave similarly to the rock dropped in the pond, creating ripples in the air pressure all around it. However these ripples will look closer to one of those “magic springs” we used to play with as children, with the movement (sound energy) being pushed all the way along the string and then back again. Such changes in pressure, when meeting our ears, will cause our eardrum to vibrate, and we will perceive them as sound.
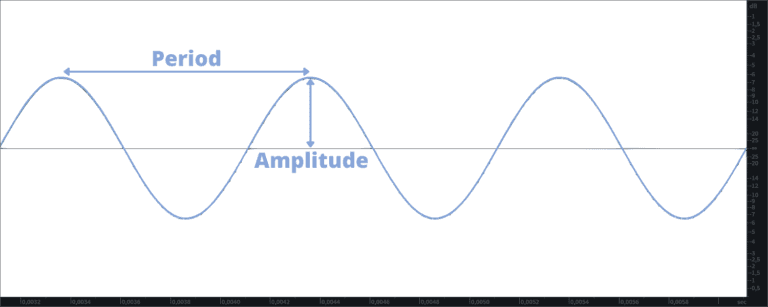
In a general sense, all these waves can be represented in a similar way: with crests (or peaks), corresponding to the ripples we see above water, in one case, and the areas of greater air pressure, in the other; and throughs, the mirrored parts below the surface or areas where the air is rarefied, that is, the pressure is lower. By measuring the difference in value (either distance or pressure) between these two max points, we obtain the amplitude of that wave – which in terms of perceived sound, indicates how loud it is.
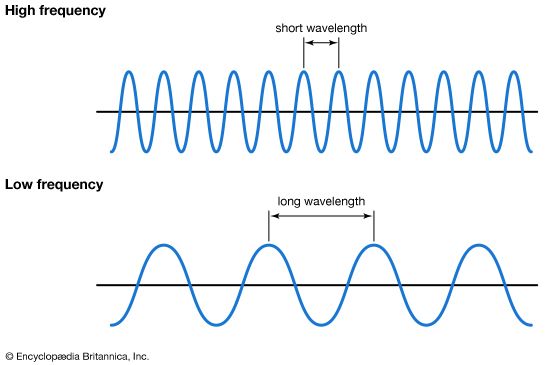
Each occurrence of a ripple and its counterpart, so each time that a wave goes from a neutral point to its crest and through and then back to neutral again, is called a cycle. The time it takes for the wave to complete one cycle takes the name of period, and the distance covered by the wave while completing it is defined as the wavelength.

All these relate to the concept of frequency, a word so much used when talking about tones, sounds, and music. The frequency of a sound is, in fact, how many times the sound wave that corresponds to that sound is able to complete its full cycle within one second. The higher the frequency, the shortest the period (time) and wavelength (distance) of the wave.


Finally, we come to the one concept that we can use to explain all secrets behind modulation pedals: that of the phase of a wave.
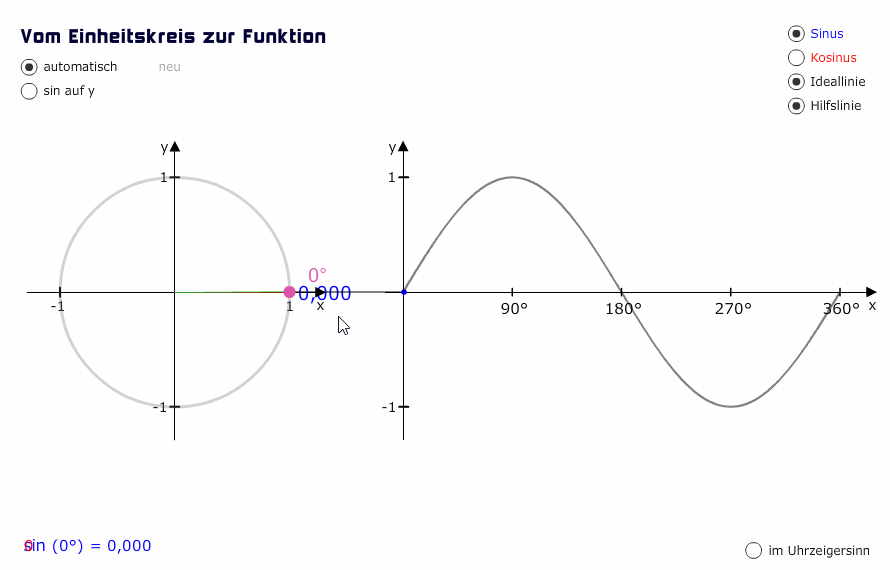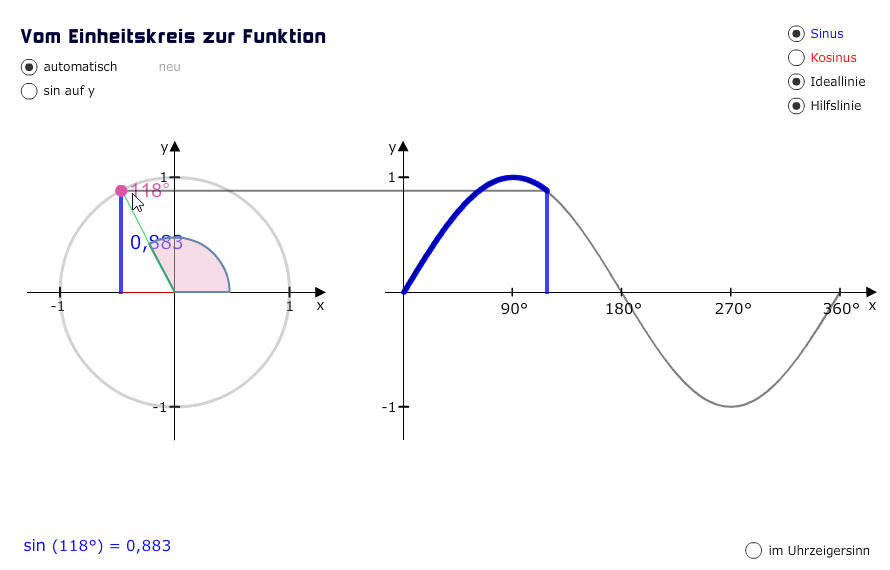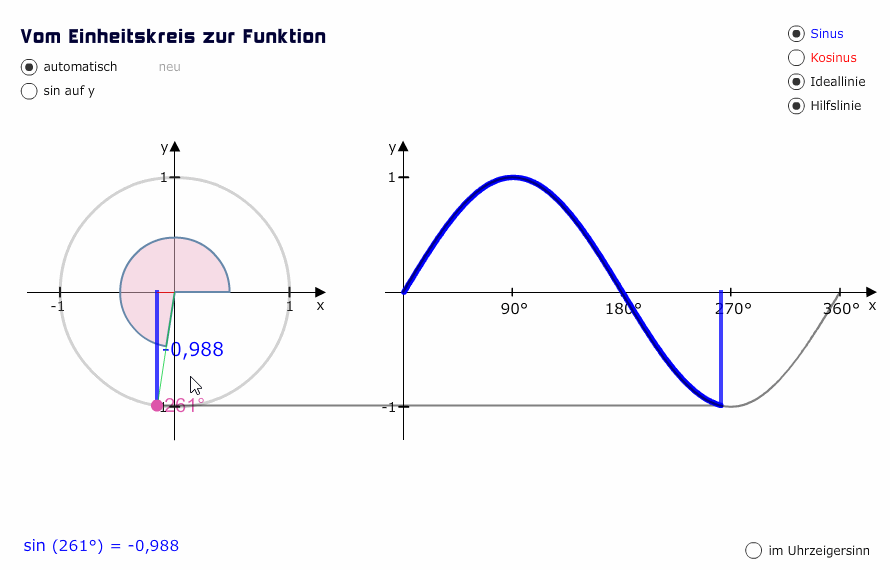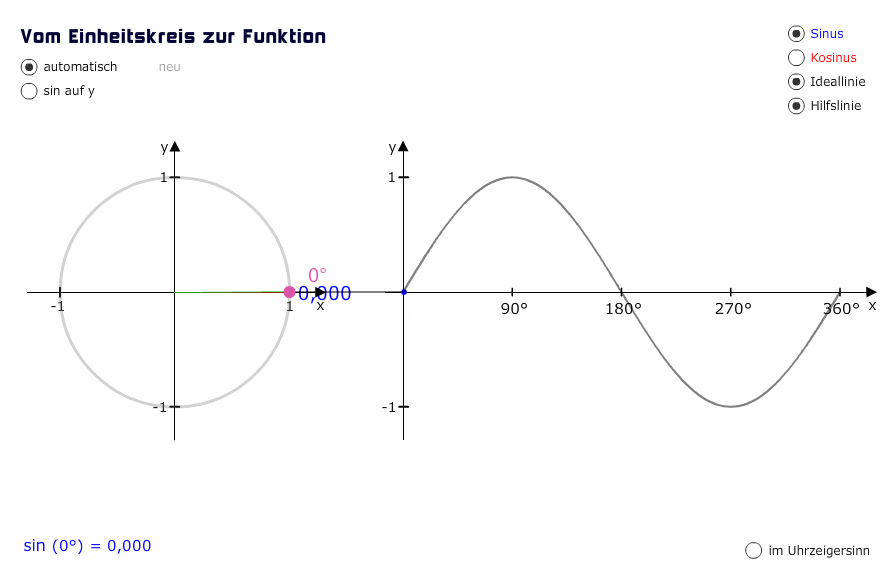
To make things clearer, we will use sine waves for our examples. Sine waves are created by a single frequency, linearly going from neutral state to their peak and then trough and back to neutral. In this case, how “steep” the wave appears, and how quickly it performs its cycle, is only influenced by its frequency.
Phase is a concept used to describe the location or timing of a point in a wave cycle, usually expressed as degrees of an angle that is measured in that literal cycle. For example, the crest point of a sine wave is 90° of its cycle, and the trough is its opposite, 270°. The moment that phase becomes really important, however, is when two waves interact with each other.
Imagine again the pebble dropped into the pond: ripples have been generated and are spreading all around, in a regular pattern. Now we drop a second identical pebble in. This pebble will also create ripples of its own, independently from the ones that were already there. Now, two possible things can happen: either the ripples “rhythm” will be roughly synchronised in time with that of the already existing ones, or the opposite will be true. In the first scenario you will see the ripples getting higher over the water. In the second, the already existing ripples and the new ones will work against each other, resulting in smaller ripples or even cancelling each other out.
A very similar situation presents itself in the case of sound waves.
Imagine two identical sine waves – same frequency (and therefore period and length), same amplitude (therefore same loudness). We will now picture two different cases, and cover the same scenarios we introduced in the pond.
First case: the two waves originate from the source exactly at the same time. In this case, their “ripples” will be completely synchronised. That means that they will reach their crests and troughs at exactly the same time, or, in phase terms, they will be at the value of 90° and 270° at the same moment. In this scenario there is a perfect synergy between the two waves. The resulting sound will consist of a third wave with an amplitude that is the sum of the amplitudes of the two waves. When two waves interact in a way that the resulting wave is more pronounced in terms of amplitude, we call this a constructive interference and we say that the two waves are in phase.

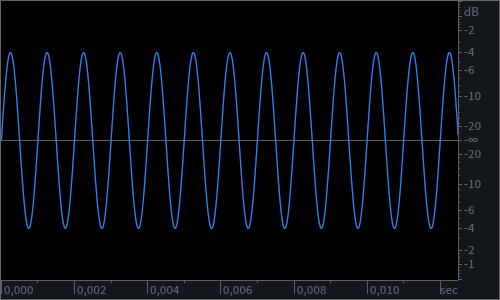






Second case: one of the two waves originates from the source after the other, but before the first one has completed one full cycle. In this case, their ripples will not be synchronised. As they move through space creating areas of increased or decreased pressure, they will reach their peak points of crest and troughs at different times. For example, when one wave will be at 90° of its cycle, the following one will maybe only be at 60°.
In other words, at any point in space and time, each wave will present an amplitude value that is not the same as that of the other. Sometimes the amplitudes will still add up constructively, causing an increase in loudness. Sometimes, instead, they will be directed in opposite “directions”, and the amplitude of the resulting wave will be smaller than that of either of the two identical waves. When two waves interact in a way that the resulting wave is less pronounced in terms of amplitude, we call this a destructive interference or we say that they are out of phase.

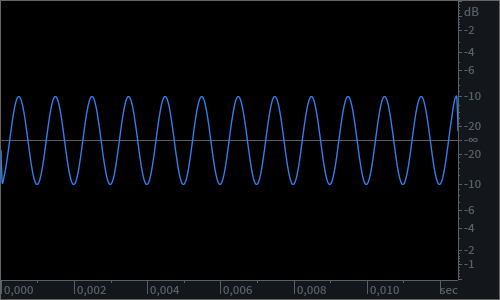
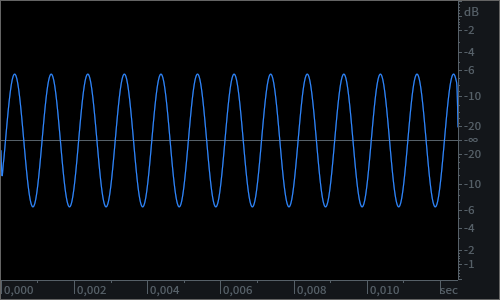






The bigger the delay between the two waves within one single cycle, the more the destructive interference, with the most destructive interaction happening when the second wave is delayed by half a period. This will result in a phase shift of 180°, or, if you picture it as on the graph below, in a situation where the phases of the two waves “mirror” each other. In this situation, at any point in space and time, the two waves will interfere with each other in a perfectly destructive way, and cancel each other out

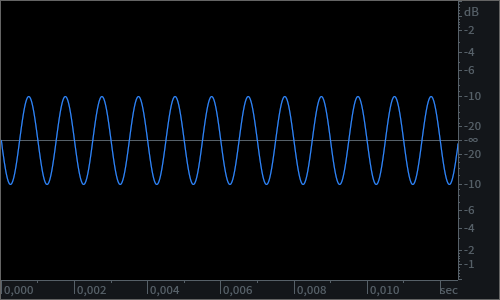






In the real world, however, we seldom – if ever – encounter situations where there will be such simple interactions as those described for identical sine waves. Each sound we perceive, is in fact a complex wave built by multiple frequencies adding on to each other in the two ways described above. In this case, however, it is not a delay in origin but the different frequency components that create “interference” with each other. As each frequency component will have a different period and wavelength, their relative phase in their cycle will also differ from that of any other frequency component, and all components will interact with each other at all points in time and space through both constructive and destructive interference.







So here we go, getting to the juice of our favourite modulation effects. As introduced in the sections above, the whole secret of modulation effects lies behind the concept of phase relations and of destructive or constructive interference between sound waves. Choruses, flangers, and phasers vary in the way they create phase shift and consequently interferences in the sound, a difference which ultimately leads to the rich variations in tone each of these effects provide. It is those mechanisms and differences that we will now look at in detail.
Among modulation effects, choruses are the ones that most try to replicate a real world phenomenon. A chorus effect is defined in music as the interaction between multiple individual sounds which share almost identical time and pitches. When such sounds converge, they’re perceived as a single tone by the human ear, characterised by a specific shimmering quality. The shimmer occurs because of “beating”, a specific type of constructive/destructive interference that happens between multiple, almost identical sounds.
A chorus pedal tries to emulate this real life effect by taking the sound fed into its input, creating a copy, and delaying the copy by a few milliseconds, before mixing the two two back together. The same process can of course be repeated with multiple copies of the sound. In order to slightly change the pitch, chorus pedals use a Low Frequency Oscillator (LFO) to modulate the delay time. This has the advantage of minimising the constructive and destructive interference, which would be more pronounced if the two delayed waves were identical.
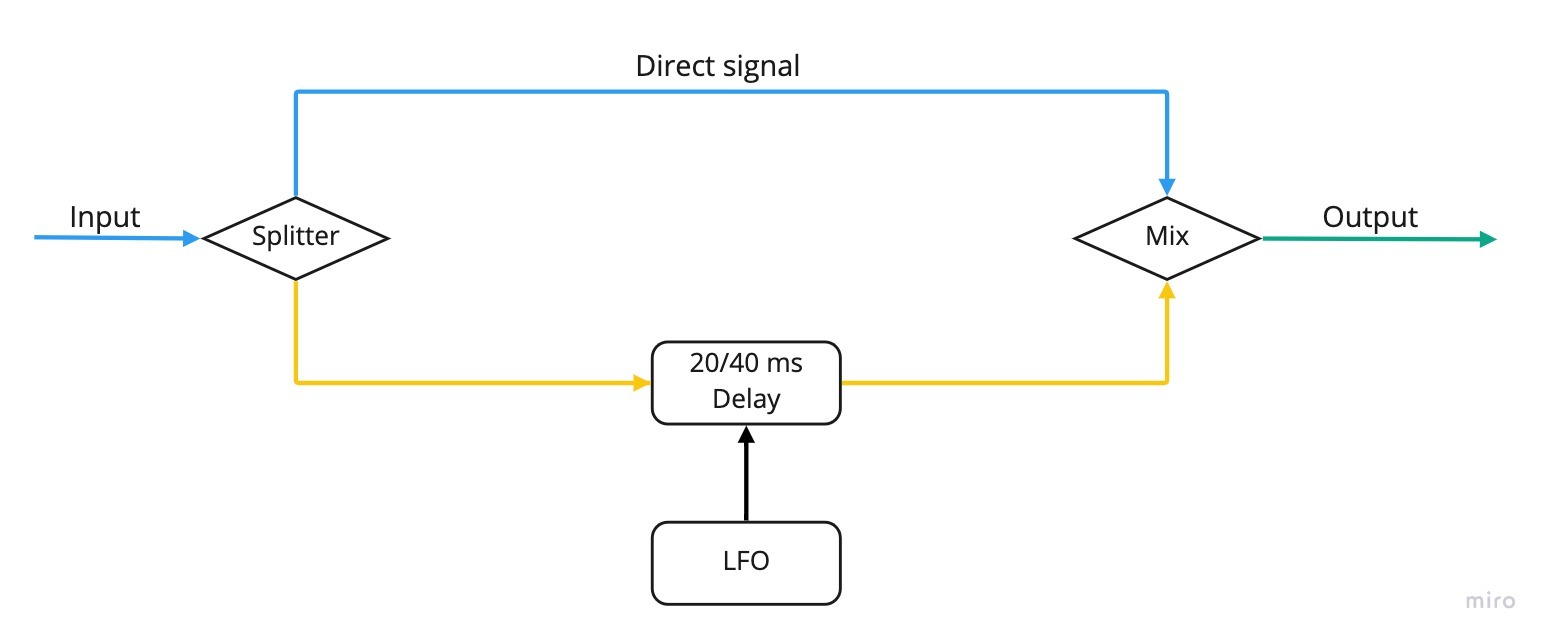
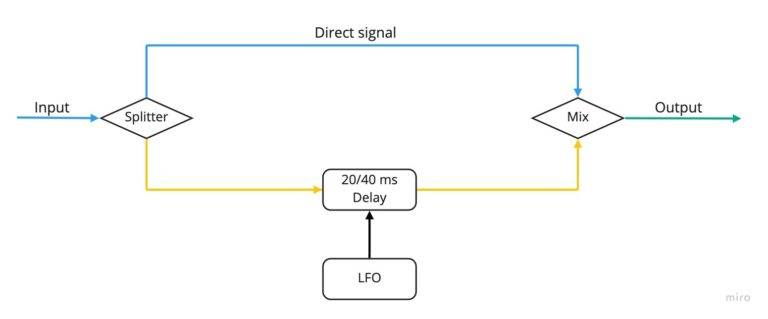
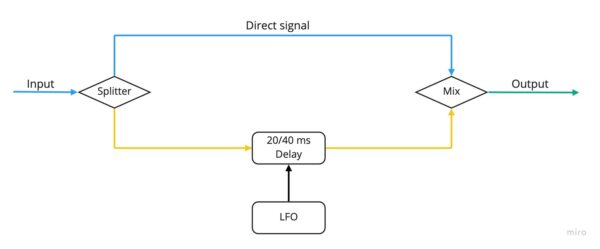
Typical settings available on such pedals include the rate of the LFO, and a mix or depth setting regulating the amount of delayed signals mixed with the original, “dry” one. In addition, chorus pedals can have the option of a stereo output. In this case the whole effect is enhanced, as the modulated copies of the signal are also slightly offset between the left and right channels, resulting in an added sense of width in the overall sound.
Some examples of chorus pedals used in great music classics are for example the Small Stone in Nirvana’s Come as You Are, MXR Choruses in Slash’s sounds such as for Paradise City, but also the historical Dimension C chorus on Prince’s voice in Purple Rain. To get an idea, you can listen to and compare all of them in the player just below.
The design of a flanger is rather similar to that of a chorus in a technical sense: flangers also create copies of the original signal and delay them, before mixing them once more with the “dry” signal. Another shared feature is that flangers also use a Low Frequency Oscillator to modulate the delay time of the copied signals. However, in comparison to choruses, the delay times introduced by flangers are much shorter, and it is this feature that is responsible for the remarkable difference in sound between the two effects. For an example, try out the chorus/flanger pedal in the player below: use the switch to move between effects and see how different they sound on the exact same pedal setting.
The very short delay times of flanger effects mean that the constructive and destructive interference between the original and its copies are maximised. Where the two sound waves add onto each other, resonances are created; but in the few places where they don’t, they almost cancel each other out, causing a series of notches (notch filters) at harmonically related intervals. Additionally, because of the shorter delay time in flangers, the notches will occur at higher frequencies on the spectrum, making them more obvious to human hearing. This type of filtering, because of its shape that you can observe in the picture below, is called “comb filtering”, and, together with the LFO modulated delay time, which “moves” the notched frequencies on the comb, creates the well known “aeroplane” resonance sweep that characterises flanger pedals.
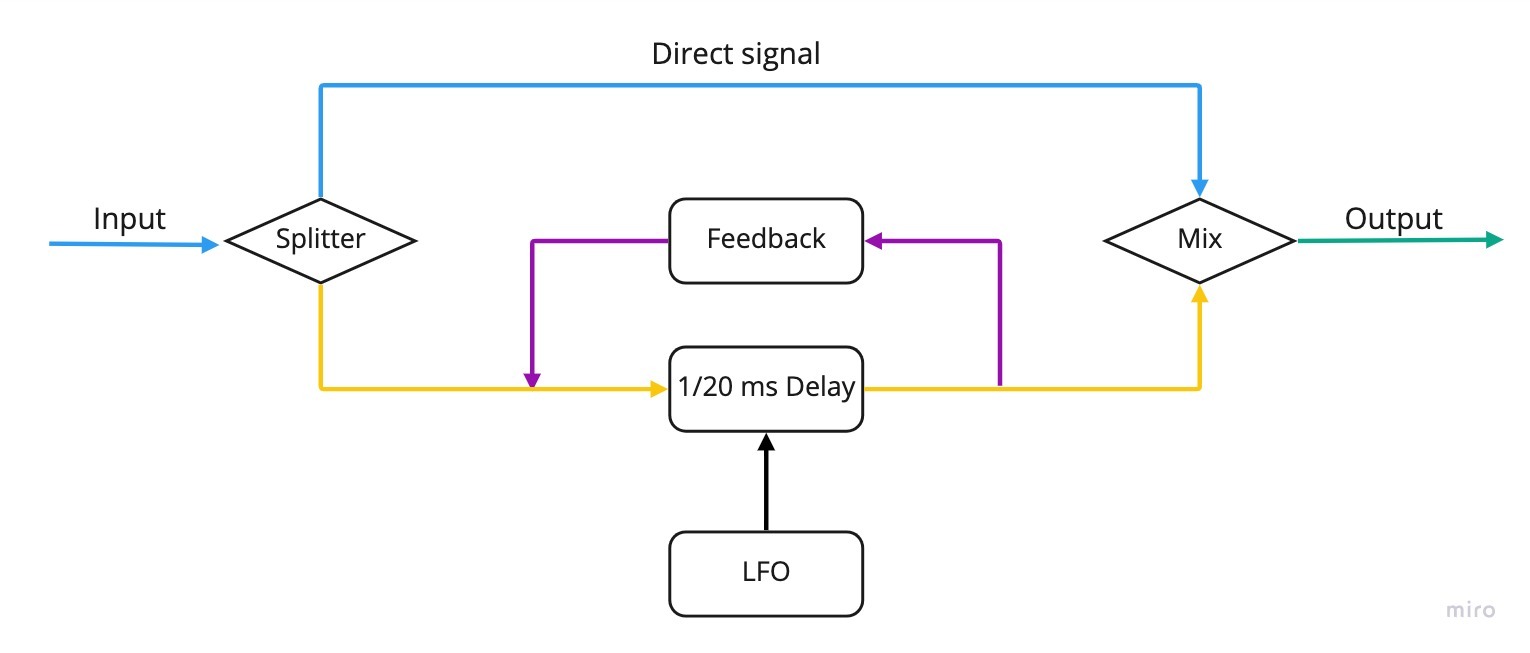
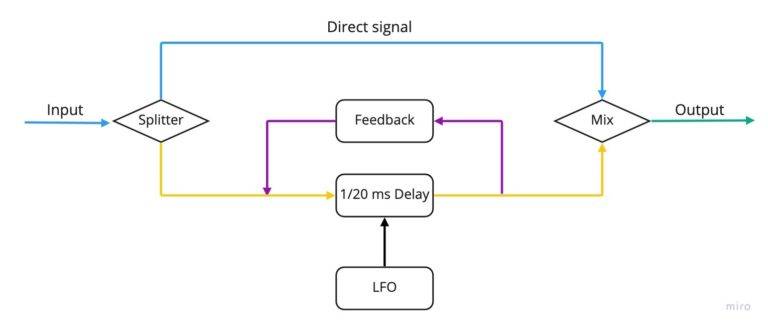
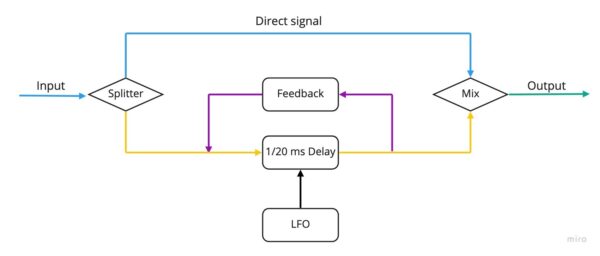
Settings on flanger pedals very often resemble and are similarly named to those on choruses. However, one additional feature of this effect pedals is the feedback: sending a copy of the signal that already went through the pedal once back to the input, so as to maximise the effect of resonances and notches, contributing to the harsh, sort of metallic timbre of these pedals.
Famous examples of flanging guitars include Jimmy Page riff in Nobodies Fault but mine, as well as the great intro of Barracuda by Heart. Check out for example how Kravits uses a flanger on some simple muted chords in the video above, or go on to compare the sound of some pedals yourself in the player just below.
Like choruses and flangers, phasers also work by duplicating the original signal. However, contrary to the other effects in this family, they don’t use delay to obtain modulation. The original signal is instead copied and passed through a series of “all pass” filters. These do not change the frequency content of the signal, but do introduce a phase shift around a certain frequency. When the signal goes through a number of such filters built in series one after another, a “comb filter” similar to those of flangers will show up.
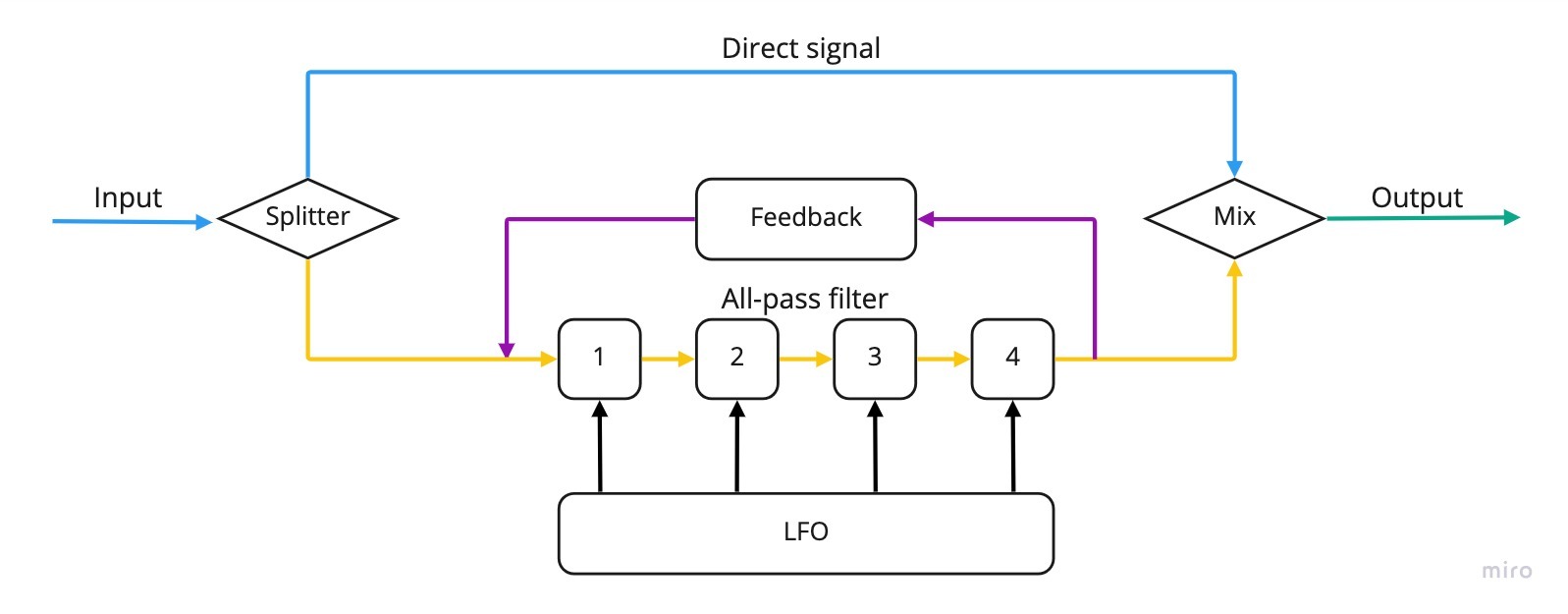
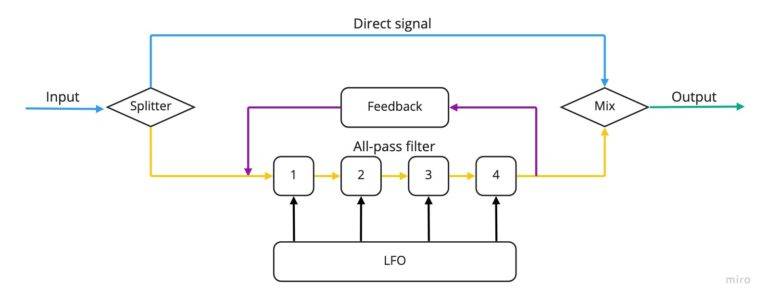
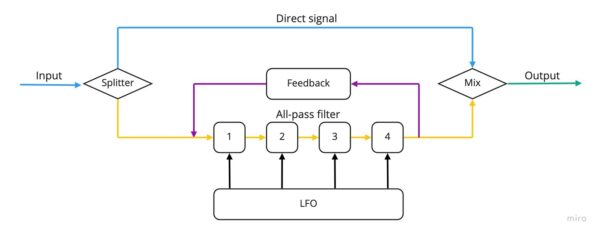
However, the teeth of the comb will depend exclusively on the filters used, and will not be related to each other harmonically, something that confers to phasers a softer tone compared to those of flangers. (spectrogram pic) Additionally, an LFO can be used also in this case in order to modulate the notches on the comb filter, obtaining a sweeping effect somewhat similar to that of a flanger.
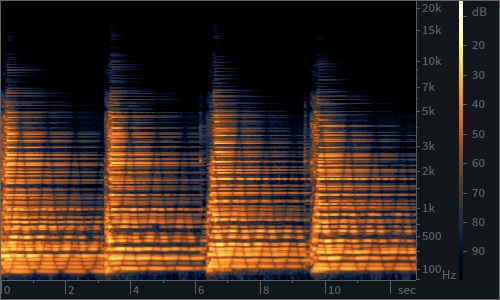
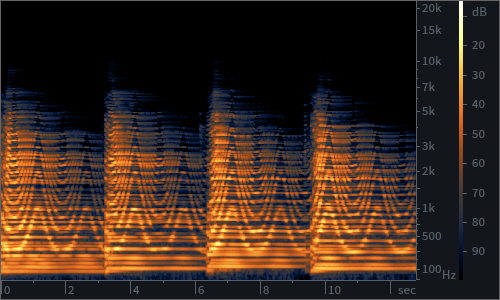




Usual controls on phasers include rate and depth such as for choruses and flangers.Sometimes a control for the cut off frequency of the filter or, in rarer cases, a feedback control similar to that of flangers is added.
Phasers have been used in famous masterpieces such as Eruption by Van Halen, where an MXR Phase 90 whooshing sound can be heard in the tapping part; the same effect can also be heard with a different character in Shine On You Crazy Diamond and Paranoid Android. To have a listen to a few phasers have a look in the player just below.
One topic often discussed when coming to modulation is – where should I place it in my effect chain?
As a rule of thumb, the classic placement of modulation would be between any distortion and before any reverb or delay .
However, playing around and experimenting with it can yield interesting results. For example, pretty much the entire genre of grunge is built around using a chorus before distortion. Bends and chords played in this setup appear to be simultaneously in and out of tune, adding sharpness to the distorted clipping. On the other hand, placing a phaser with a slow rate before a drive pedal can make power chords sound like a roaring lion. While, on the other end of the chain, putting a phaser or a flanger after a delay can produce an interesting filtering effect on the delay repetitions, making sure each stands out tonally.
Below, you can find a great example of a pedal that not only incorporate different types of modulation together with fuzz distortion, but lets you swap the order of the effects in the chain. Play around and find new creative ways of shaping your tone!

Klon or Klones? A legend under the lens
Few pedals exist out there whose legendary status and hype have peaked as high as that of Klon’s Centaur overdrive. This pedal, worth a couple

As the first guitar pedals hit the market back in the 1960s, they did it as encumbering, hefty boxes that looked as gritty as they